Written by Stephen Baek
on 

Geometric Data Analysis - Ep.1: Bottom of your running shoes

If you have ever visited the University of Virginia (UVA) grounds (we call it the ‘grounds’ for some reason, instead of the common term ‘campus’), odds are that you might have walked by a shoe store called ‘Ragged Mountain Running & Walking Shop.’ As one may be able to infer from their motto, “Central Virginia’s Community Running and Walking Headquarters since 1982,” it seems like a lot of Charlottesvillians have plenty of fond memories and even some pride about this store that has been around for 40 years. To say the very least, the place is definitely one of the local landmarks of the Charlottesville area, as you can learn more about the shop’s interesting history from this UVA Today article. Strangely enough, the UVA School of Data Science, which I’m affiliated with as a faculty member, happens to be situated on the second floor of the historic shoe store. So, I thought the main topic of this first episode of the ‘geometric data analysis’ blog post series could be some interesting stories about shoes.


The historic shoe store on the UVA grounds. The School of Data Science happens to be situated on the second floor of the same building. (Image Source: UVA Today)
 

Shoes that rock

I don’t know how many of you have happened to take a moment of your life to seriously ponder why shoes look like what they look like, but I would bet only a few have done so. This in fact would probably be a silly question to many people, because, you know, shoes are shoes! However, the shapes of shoes are quite an interesting subject to geometers like myself, as there is actually much more interesting science behind their shapes. Let me tell you a story. There once was a time when this thing called ‘Masai Barefoot Technology (MBT)’ shoes or more casually ‘Masai Walking’ shoes was a trend. For those of you who don’t recall exactly what those shoes were all about, or are too young to hear of them, Masai walking shoes are a sort of funny-looking shoes that have round soles (as opposed to other ‘flat’ regular shoes). They went viral because of the belief (and largely marketing, of course) that their signature round soles could actually improve balance and posture during the walk, improve blood flow, reduce lumbar pain, and increase muscular activities.1 They made claims that their meticulously designed curvature could produce a natural rolling motion, similar to the foot movement when you walk barefoot on sand, dirt, or grass. This is how our archaeological ancestors used to walk and what our body had adapted to through evolution, and therefore, it must beneficial to our musculoskeletal system (aka, muscles and bones) than the ‘unnatural’ motion caused by conventional shoes—was kind of the thought process there.

Rocker bottom shoes, also famously known as ‘Masai shoes.’ (Image Source: Wikipedia)
 

Soon after their debut, quite a few serious scientific studies actually came out, supporting the shoe manufacturer’s claims on the health benefits. For instance, Stewart, Gibson, and Thomson (2007) suggested that Masai shoes could reduce the peak pressure applied under the midfoot and the heel, and therefore might be useful to people with flat feet, obesity, etc.2 Stöggl et al. (2010) also suggested that those MBT shoes were mechanically unstable and thus provoked increased variability of movement during walking,3 meaning, (*and hereafter is my interpretation) such instability and movement variability could promote the use of more muscles and thereby train them better and burn more calories. Some studies further suggested that MBT may reduce pain and discomfort in the lower back4 and lower extremities5. To all fairness though, these results are quite controversial. For one, all of these authors were financially supported by MBT and/or other related private entities. There were also plenty of other scientific studies that warn of the risk of falls and overuse injuries6,7 or deny the benefits of training leg muscles and burning extra calories.8 The National Institute for Health and Care Excellence (NICE) in the U.K. even states in its guideline that “when rocker sole shoes were compared with flat sole shoes no benefit was observed favouring rocker sole shoes for any of the reported outcomes in either the short or long term follow-up. It was noted that health-related quality of life was in fact, worse in the rocker sole group at both the short and longer term time points” and therefore, healthcare professionals should not offer these kinds of shoes as a treatment for lower back pain or sciatica.9 Nevertheless, one thing seems to be abundantly clear: the shape of the sole does influence the biomechanics of how you walk.


Shoes and mozzarella cheese

In 2013, Nike, one of the world’s largest sportswear manufacturers, filed a patent application titled “Auxetic Structures and Footwear with Soles Having Auxetic Structures.”10 One thing that is quite prominent in their application is the interesting geometric pattern at the bottom of the shoes. This repeating pattern of triangles is indeed what’s referred to as “auxetic structures.” Here, the word ‘auxetic’ is an adjective form of ‘auxesis’ meaning the “increase of cell size without cell division,” according to the Merriam-Webster Dictionary. Yes, I know. The dictionary definition is not so helpful. In fact, to understand the actual meaning of the term, we’ll need to take a deeper look into some basic mechanics and elasticity theory (yikes!).


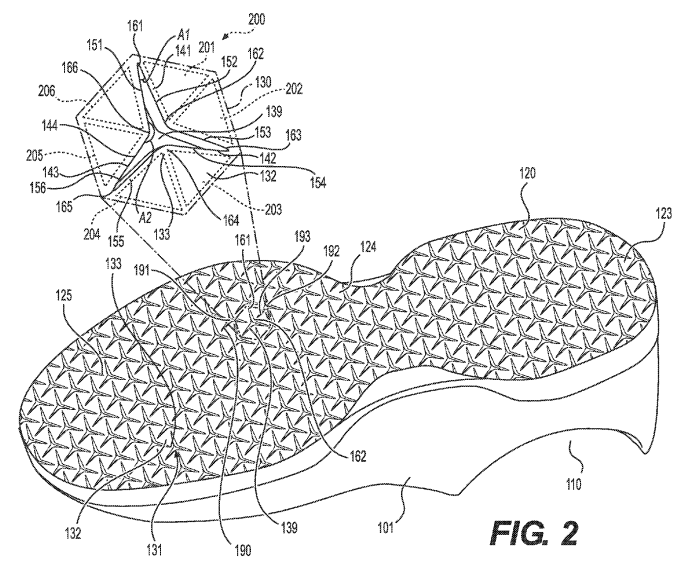Nike’s patent on auxetic sole patterns. (Image Source: Cross et al. United States Patent, No. 9,402,439 B2)
 


‘Auxetic’ pattern on a running shoe. (Image Source: Wikipedia)
 

Personally, I think the best way to understand the elasticity theory is to think about mozzarella cheese, because, you know, who doesn’t like mozzarella cheese?! Imagine a hot mozzarella stick freshly out of the oven (yum!). To whet your appetite, visualize stretching the mozzarella stick with your hands. Do you see that absolutely stunning visual of stretchy-melty-cheesiness in the middle? The longer you stretch, the thinner your cheese is going to get, turning into almost like a thin string. Conversely, when you compress the cheese stick with your fingers, the cheese will bulge out of your fingers, growing larger in the direction perpendicular to the pressure. Not only mozzarella cheese but, as a matter of fact, almost all materials around us have the similar property of getting thinner when they are stretched and getting thicker when they are compressed, just like the mozzarella stick you just visualized.

The more you think about it, the lesser this phenomenon starts to make sense. Think about it. When you stretch a mozzarella stick, the force is applied along the axial direction, or the length direction, of the mozzarella stick. So it would be more intuitive to think that the deformation would happen along the direction of the force. However, why would the cheese deform perpendicular to the direction of the force? Similarly, when you squeeze the cheese with your fingers, the force is applied along the imaginary line connecting your fingers. However, the cheese will deform orthogonal to the direction of the force, as we already know from numerous of our experiences. Did we miss something?


A counter-intuitive deformation of a mozzarella stick. (Image Source: 30 Minutes Meals)
 

This is in fact the same question that physicists were working on in the nineteenth century. A British polymath Thomas Young (1773-1829) is perhaps one of the most important names in the elasticity theory. In his 1807 work, ‘A Course of Lectures on Natural Philosophy and the Mechanical Arts,’ Young described that “we may easily observe that if we compress a piece of elastic gum in any direction, it extends itself in other directions; if we extend it in length, its breadth and thickness are diminished.” (*I wish there were mozzarella sticks in his era!) In fact, Young and the fellow scientists of his era described referred to this phenomenon as ‘stretch-squeeze ratio.’ However, the first to derive a more rigorous, quantitative definition was a French mathematician and physicist, Siméon Denis Poisson (1781-1840).

In 1827, Poisson published a note,11 in which he formally defined the stretch-squeeze ratio as the ratio ‘ν’ (nu). In today’s modern mechanics, Poisson’s ratio is defined as the negative of the amount of transversal deformation divided by the amount of axial deformation (*more rigorous definition involves the notion of ‘strain,’ but that would be way beyond the scope of this post). Here, the term ‘axial deformation’ means either stretch (+) or compression (-) of mozzarella cheese whereas the term ‘transversal deformation’ means the perpendicular squeeze (-) or bulging (+) as a result of the axial deformation. Solids occurring in nature usually have the Poisson’s ratio between 0 and 0.5. Steel, for example, has a value of around 0.3, whereas gold has a value near 0.4. A larger value means that the ‘stretch-squeeze’ effect is more dramatic. Mozzarella cheese has a Poisson’s ratio a little shy of 0.5.12 The value of 0.5 (e.g. water) means that the material is perfectly incompressible. It is impossible for solids to have a value of 0.5 or greater. A funny thing here is, Poisson believed that the ratio was constant for all materials, which is why I said “in today’s modern mechanics” when I introduced the definition of Poisson’s ratio above. While many people believe that the name of the ratio is a tribute to Poisson, it is rather quite opposite. A few decades after Poisson’s note was published, the physics community collected more evidence that the ratio was indeed different across different materials, and the name, Poisson’s ratio, was used as a way of referring to the flawed theory.13 I guess the moral of the story here is ‘time makes your epic mistake eventually a tribute,’ so don’t be afraid of making mistakes!

At this point, I guess some of you are already scratching your heads thinking ‘Why is this guy keep talking about all these mozzarella cheese and nerdy ratios and stuff? Wasn’t this supposed to be a blog post about shoes?’ No, you are absolutely right. The reason for the side track was in fact to give you enough of a background to explain ‘auxetic’ materials. Simply speaking, auxetic materials are the materials that have negative Poisson’s ratios, now that we know a thing or two about the Poisson’s ratio. But wait a second, didn’t I say that solids can have a Poisson’s ratio between 0 and 0.5? How is it possible for a solid to have a negative Poisson’s ratio? What does it even mean to be negative? Well, a negative Poisson’s ratio simply means that a material will deform in an opposite way than what a mozzarella cheese would do. In other words, auxetic mozzarella cheese would get thicker and thicker as you stretch it, and would get thinner and thinner as you compress it.

Auxetic materials are extremely rare in nature. Certain rocks and minerals are known to have negative Poisson’s ratios. The skin covering a cow’s teats is also known to be auxetic.14 However, scientists discovered a few ways to synthesize auxetic materials. The discovery of Gore-Tex is one such example. Wilbert Gore and his son Robert Gore discovered the functional fabric by stretching heated polytetrafluoroethylene. This new fabric is known to possess a negative Poisson’s ratio,15 among other nice properties such as breathability (i.e. impenetrable for liquid water, but not for vaporized water molecules), heat insulation, etc. It is understood that the microporous (=lots of small holes that are only visible under a microscope) structure filled with air plays the crucial role of producing the auxeticity. However, the discovery of Gore-Tex was rather a serendipity, in which the son Bob Gore gave a hard yank to heated polytetrafluoroethylene with a sudden force out of frustration after a series of failed experiments.16

A more meticulously calculated way to turn a regular material into an auxetic material can be found in Grima and Evans’ letter17 to the Journal of Material Science Letters. Grima and Evans’ main idea was to connect squares at their vertices in a configuration displayed in the figure below.


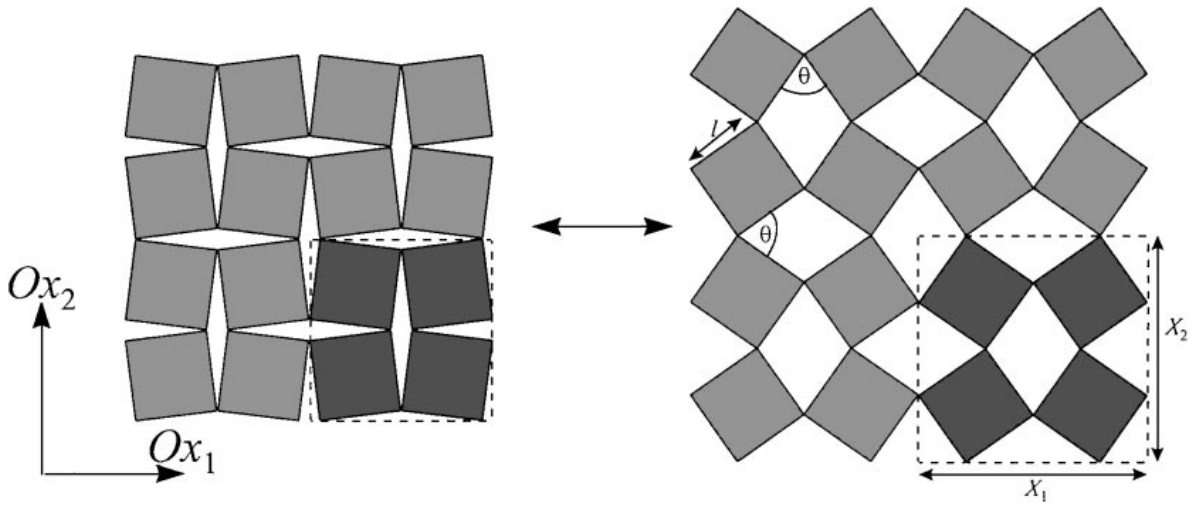The auxetic “rotating squares” structure. (Image Source: Grima & Evans, 200017)
 

The geometric pattern on the Nike’s auxetic sole patent is essentially a triangle version of Grima and Evans’ rotating squares structure presented in the same letter. Theoretically, the rotating triangle structure has the Poisson’s ratio of -1,17 although this calculation is based on an ideal, mathematical setting. Nonetheless, this is a brilliant way of turning literally any solid material into an auxetic material, as being demonstrated by Konakovic et al. (2016)18 on a sheet of plastic:

“Rotating triangles” turns a plain sheet of plastic into a cool auxetic material. (Source: Konakovic et al. 2016)
 

Why did Nike even bother to create this structure at the bottom of their running shoes? Well, that’s because the auxetic deformation can better accommodate the natural deformation of your feet. When you strike your foot on the ground as you run or walk, the sole of your shoe is going to be bent and stretched. Now, if you were to build a shoe sole with a regular rubber, the rubber will get thinner with the stretch and apply more pressure, making your shoe feel tighter on your foot and overall uncomfortable and fatiguing as you make more steps. However, thanks to the auxetic structure, your shoe will expand and get fatter instead of thinner, and accommodate your foot much better. Pretty cool, huh?

Auxetic soles expand in width and length to better accommodate the natural deformation of your feet. (Source: Nike)
 


Metamaterials via geometric data analysis

‘Metamaterials’ is a term used in the scientific community to refer to materials with novel material properties. The term originates from the Greek word ‘meta (μετά)’ meaning “beyond.” (*‘Beyond-materials’… what a cool name!) A popular way of producing metamaterials is by creating some repetitive geometric patterns like what we saw from the auxetic shoe sole example. Of course, not all shapes and patterns would give us a cool property. Now, if you are a material designer, you would need to run numerous experiments with a variety of different shapes and arrangements until you discover the specific shape and arrangement that produce the desired property. The bad news here is that there can be literally infinitely many possibilities of shapes and arrangements you can choose from, if you think about it. This means that you will need to swim in the ocean of infinite possibilities (we call this ocean, the ‘design space’) with a spoon of wishful thinking that you will someday find a treasure chest somewhere deep down the sea. This obviously doesn’t sound like a terribly good idea. And this is where data science can be quite useful (and this is where the good news begins).

Assuming that you have a sufficient number of observations (i.e. data points) on shapes and their corresponding physical properties (e.g. Poisson’s ratio), you can create a machine learning model that captures the relationships between shapes and physical properties. For those of you who are not familiar with data science jargon, a ‘model’ is essentially a mathematical function that takes certain inputs (called ‘independent variables’) and spits out certain outputs (called ‘dependent variables’). In our case, the inputs would be some parameters describing shapes (e.g. height, width, diameter) and the outputs would be physical properties that the input geometry may exhibit. If you have a perfectly “accurate” model, the model will tell you exactly what is going to happen for a given shape. In actuality, a model almost always possesses some errors. But still, even with the presence of prediction error, you can rely on your model to explore the design space (i.e. all possible shapes). This can be a great benefit, because usually material experiments, regardless of whether you are talking about computer simulations or lab experiments, are incredibly time-consuming, laborious, and costly. With a model, however, all you need to do is to just enter some shape parameters into the model and the model will tell you right away what’s going to happen. Since computers are super powerful these days, you can make hundreds of thousands of predictions for different shapes in just a few hours. So the idea is to let computers automatically generate some random shapes, feed them into a model, predict their physical properties, and repeat this process until it stumbles upon something. While your computer is doing all these works, you can go out for a cup of coffee, hit some golf balls, or do whatever your free time hobby is. Sounds like a pretty sweet deal, huh?

Of course, like every other thing in our lives, there’s no free lunch. Building an accurate and reliable model takes a lot of effort. Despite all the efforts, your model may still struggle to make a good prediction on shapes it has never seen before. And because of this reason, you actually need to babysit your model quite a bit by validating the prediction results against actual experiment data, updating the model with new observations, etc. (Sorry no more coffee or hitting golf balls!) Despite all this babysitting, your life would be perhaps a hundred times better with a machine learning model, compared to “cut-and-try” experiments you would need to do if there were no model. The video below (see from 1:00 if you are in a hurry) is a great example of amazing things you could do with a data-driven model. The authors not only custom-designed geometric structures for target physical properties but also were able to even “program” the physical properties of those 3D objects so that they vary across different locations.

Computational design of elastic structures. (Source: Schumaker et al. 201519)
 

Conclusion

In this first episode, we looked into some interesting roles played by shoe shapes and dove a little deep into the fascinating science of metamaterials. As we saw, data science holds a key to the successful exploration of material designs. To this end, geometric data analysis, as the science of processing and analyzing geometric data (i.e. lots of shapes!), finds lots of exciting opportunities to further the current materials research to the next level. Applications are limitless: personal protection equipment (e.g. football helmets); aircrafts; optics; acoustics; fashion; you name it. Especially, with the new deep learning and AI technologies, computers’ visual cognition has become ever more capable. Not only that, but AI models are now also pretty good at creating new visuals such as fake photographs or paintings. With all these, AI may soon be able to take care of a great deal of tasks of material scientists and engineers. This, in fact, is already happening, as can be evidenced in various scientific articles, including some of my group’s works. Who knows? Not too far from now, my kid may get AI-designed water-resistant, invisible, light-emitting super-duper sneakers that allow her to jump 20 feet for a Christmas present!



References

  1. MBT Official Website, https://www.mbt.com/global/mbt-technology (Accessed: November 2, 2022) ↩

  2. Stewart, L., Gibson, J.N.A., & Thomson, C.E. (2007). In-shoe pressure distribution in “unstable” (MBT) shoes and flat-bottomed training shoes: A comparative study. Gait & Posture, 25(4): 648-651. doi:10.1016/j.gaitpost.2006.06.012 ↩

  3. Stöggl, T., Haudum, A., Birklbauer, J., Murrer, M., & Müller, E. (2010). Short and long term adaptation of variability during walking using unstable (MBT) shoes. Clinical Biomechanics, 25(8), 816–822. doi:10.1016/j.clinbiomech.2010.05.012 ↩

  4. Nigg, B. M., Davis, E., Lindsay, D., & Emery, C. (2009). The Effectiveness of an Unstable Sandal on Low Back Pain and Golf Performance. Clinical Journal of Sport Medicine, 19(6), 464–470. doi:10.1097/jsm.0b013e3181c0a96f ↩

  5. Nigg, B., Hintzen, S., & Ferber, R. (2006). Effect of an unstable shoe construction on lower extremity gait characteristics. Clinical Biomechanics, 21(1), 82–88. doi:10.1016/j.clinbiomech.2005.08.013 ↩

  6. Maffiuletti, N. A. (2012). Increased lower limb muscle activity induced by wearing MBT shoes: physiological benefits and potential concerns. Footwear Science, 4(2), 123–129. doi:10.1080/19424280.2012.668949 ↩

  7. Albright B. C. & Woodhull-Smith W. M. (2009). Rocker bottom soles alter the postural response to backward translation during stance. Gait & Posture, 30(1): 45–49. doi:10.1016/j.gaitpost.2009.02.012 ↩

  8. Santo, A. S., Roper, J. L., Dufek, J. S., & Mercer, J. A. (2012). Rocker-bottom, profile-type shoes do not increase lower extremity muscle activity or energy cost of walking. Journal of Strength and Conditioning Research, 26(9): 2426–2431. doi:10.1519/JSC.0b013e31823f8b71 ↩

  9. National Institute for Health and Care Excellence. (2016). Low back pain and sciatica in over 16s: Assessment and management. NICE guideline NG59. https://www.nice.org.uk/guidance/ng59/chapter/Recommendations (Accessed: November 2, 2022) ↩

  10. Cross, T. M., Hoffer, K. W., Jones, D. P., Kirschner, P. B., Langvin, E., & Meschter, J. C. (2016). Auxetic structures and footwear with soles having auxetic structures. United States Patent, No. 9,402,439 B2. ↩

  11. Poisson, S. D. (1827). Note sur l’Extension des Fils et des Plaques élastiques. Annales de chimie et de physique, 36: 384–387. ↩

  12. Hort, J., Grys, G., & Woodman. J. (1997). The relationships between the chemical, rheological and textural properties of Cheddar cheese. Le Lait, 77(5): 587-600. ↩

  13. Greaves, N. (2013). Poisson’s ratio over two centuries: challenging hypotheses. Notes & Records of the Royal Society, 67: 37-58. doi:10.1098/rsnr.2012.0021 ↩

  14. Lees, C., Vincent, J. F. V., & Hillerton, J. E. (1991). Poisson’s ratio in skin. Biomedical Materials and Engineering, 1(1): 19-23. doi:10.3233/BME-1991-1104 ↩

  15. Cherfas, J. (1990). Stretching the point: New materials that get fatter—rather than thinner—when they’re stretched may have some revolutionary implications. Science, 247(4943): 630. doi:10.1126/science.247.4943.63 ↩

  16. Science History Institute - Robert W. Gore. https://www.sciencehistory.org/historical-profile/robert-w-gore (Accessed: November 24, 2022) ↩

  17. Grima, J. N. & Evans, K. E. (2000). Auxetic behavior from rotating squares. Journal of Materials Science Letters, 19: 1563–1565. doi:10.1023/A:1006781224002 ↩ ↩2 ↩3

  18. Konaković, M., Crane, K., Deng, B., Bouaziz, S., Piker, D., & Pauly, M. (2016). Beyond developable: computational design and fabrication with auxetic materials. ACM Transactions on Graphics, 35(4): Article 89. doi:10.1145/2897824.2925944 ↩

  19. Schumacher, C., Bickel, B., Rys, J., Marschner, S., Daraio, C., & Gross, M. (2015). Microstructures to control elasticity in 3D printing. ACM Transactions on Graphics, 34(4): Article 136. doi:10.1145/2766926 ↩