ZerNet

Zernike Convolutional Neural Networks on Arbitrary Surfaces

Zhiyu Sun ¹, Ethan Rooke ², Yusen He ¹, Jia Lu ³, and Stephen Baek ^1
1 Department of Industrial and Systems Engineering, The University of Iowa
² Applied Mathematical and Computational Sciences, The University of Iowa
³ Department of Mechanical Engineering, The University of Iowa
{zhiyu-sun, ethan-rooke, yusen-he, jia-lu, stephen-baek} (at) uiowa (dot) edu

 

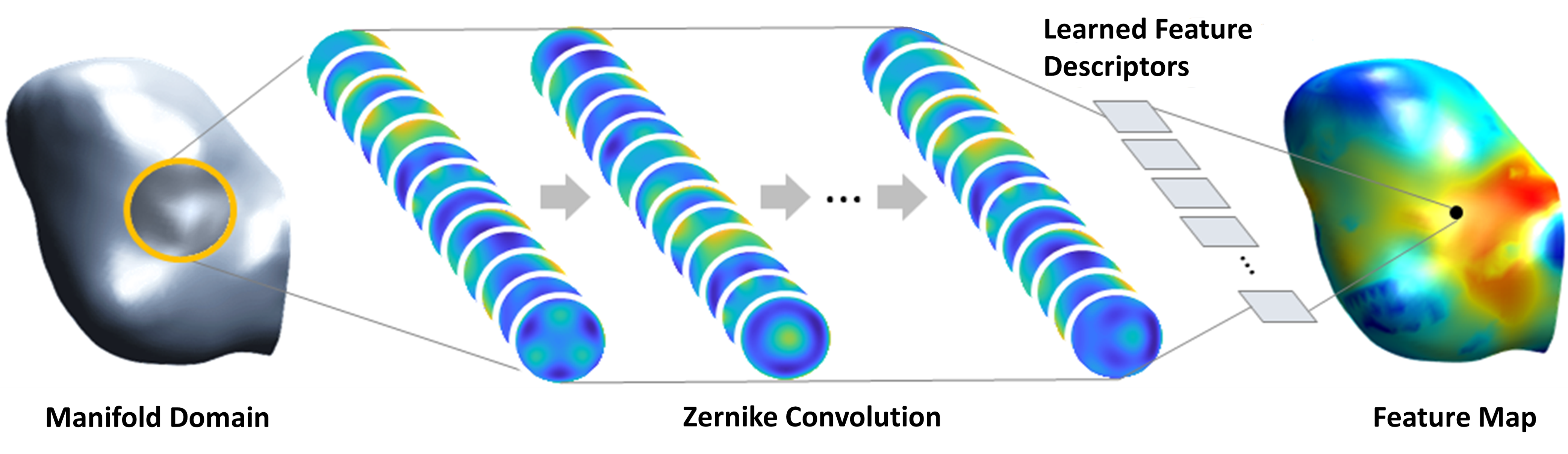
Abstract

In many fields of science and engineering, geometric features play a key role in understanding certain quantity or phenomena. Thus, an ability to codify geometric features into a mathematical quantity can be critical. Recently, convolutional neural networks (CNNs) have been shown to possess a promising capability of extracting and codifying features from visual information. However, the application of such capable CNNs has been quite limited to mostly computer vision problems where the visual information is inherently given on a grid-like structure. This, unfortunately, was not the case for the geometry processing community, where many visual recognition problems are defined on arbitrary surfaces (2D-manifolds). Technical difficulties hindering the generalization of CNNs to arbitrary-shaped manifold are rooted in the lacks of such key elements including the canonical grid-like representation, the notion of consistent orientation, and a compatible local topology across the domain. Unfortunately, except for a few pioneering works, only very little has been studied in this regard. To this end, in this paper, we propose a novel mathematical formulation to extend CNNs onto two-dimensional (2D) manifold domains. More specifically, we approximate a tensor field defined over a manifold using orthogonal basis functions, called Zernike polynomials, on local tangent spaces. We prove that the convolution of two functions can be represented as a simple dot product between Zernike polynomial coefficients. We also prove that a rotation of a convolution kernel equates to a set of $2\times2$ rotation matrices applied to Zernike polynomial coefficients, which can be critical in manifold domains. As such, the key contribution of this work resides in a concise but rigorous mathematical generalization of the CNN building blocks. Furthermore, comparative to the other state-of-the-art methods, our method demonstrates substantially better performance on both classification and regression tasks.

Keywords: Geometric deep learning, non-Euclidean data, Zernike convolution, manifold convolutional neural networks

 

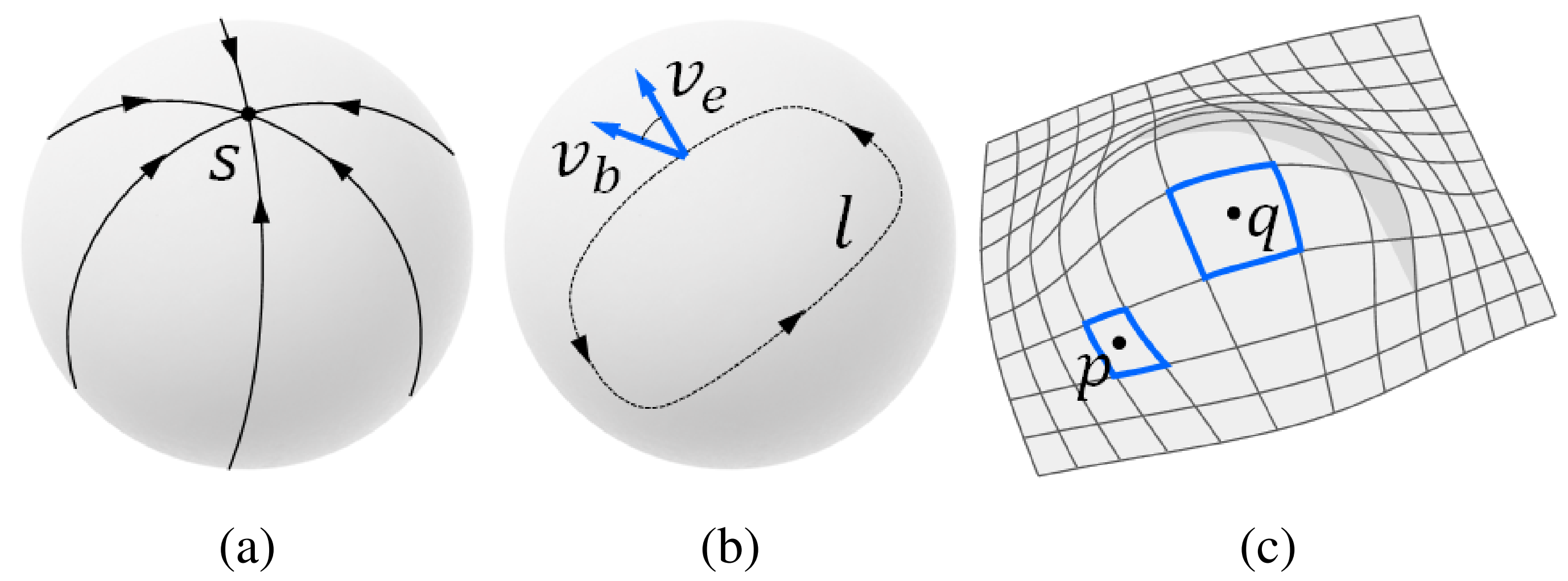Figure 1. Problems associated with manifolds when expanding the notion of convolution. (a) a topological sphere cannot have a grid defined on it without a singularity ($S$); (b) a vector ($v_b$) parallel-transported along a loop ($l$) on a manifold might end up in a different orientation ($v_e$); (c) irregularity of a grid causes varying-size receptive fields.
 

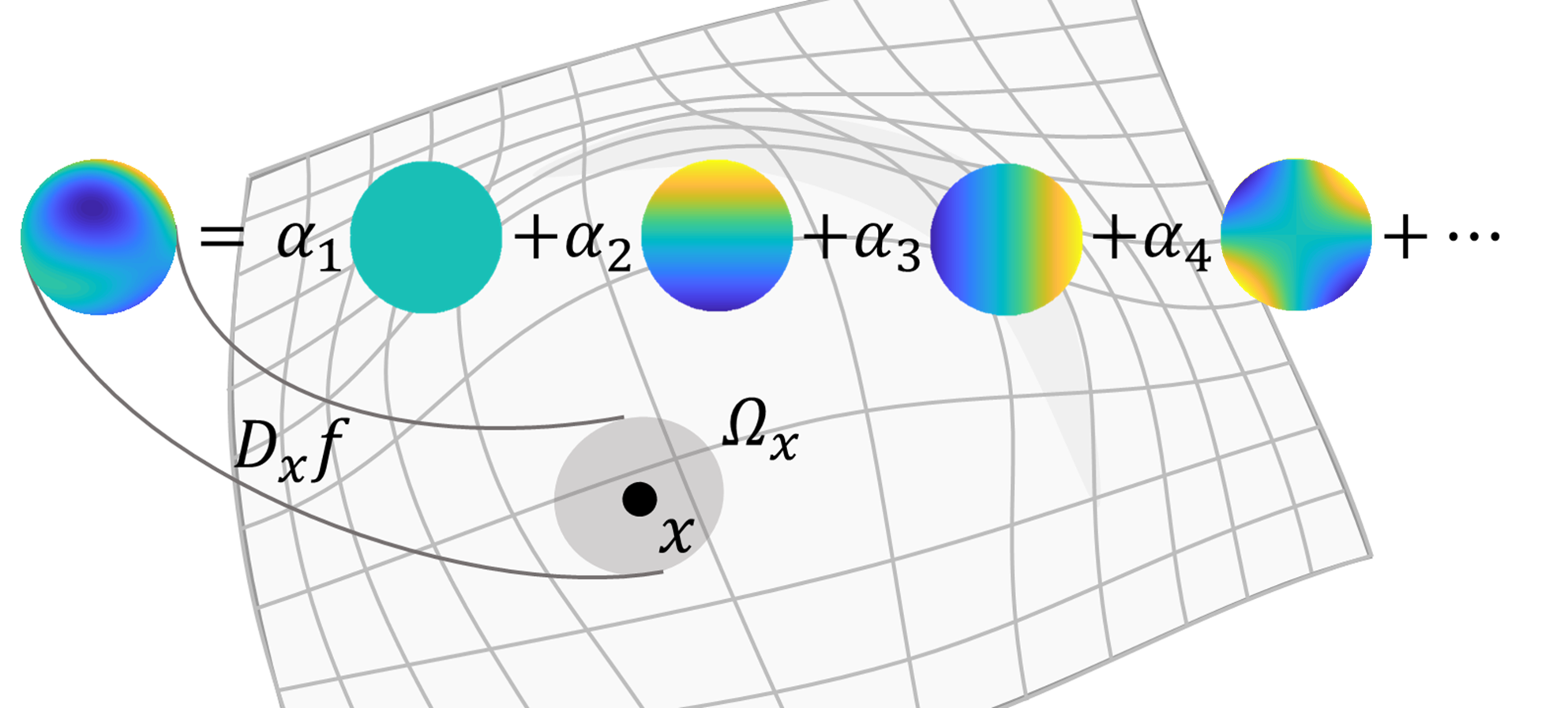Figure 2. Zernike decomposition of a function.

 

Figure 3. Point-wise geodesic error (in percentage of the shape diameter) of ZerNet vs FeaStNet on the FAUST human dataset.

 

Publications

Journals & Proceedings

1. ZerNet: Convolutional Neural Networks on Arbitrary Surfaces via Zernike Local Tangent Space Estimation
   Sun, Z., Rooke, E., He, Y., Lu, J., & Baek, S.
   arXiv:1812.01082
   Working Paper

Conference Presentations

1. Wall stress estimation in cerebral aneurysm via geometric convolu-tional neural network
   Baek, S., Sun, Z., & Lu, J.
   In The 8th World Congress of Biomechanics (WCB2018), Dublin, Ireland, July, 2018.

 

Downloads

PDF

Source Code: Will be available soon.